
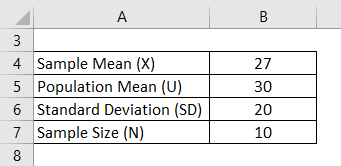
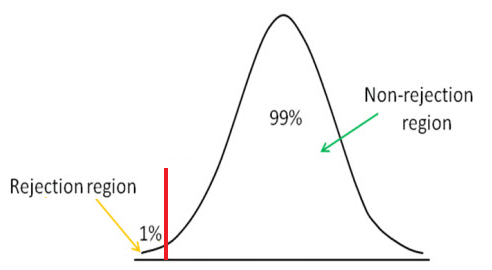
To determine the z-value, we need to first calculate the standard error. To start, we can state the null and alternative hypotheses : Assuming a significance level of p < 0.05, is the company correct in accepting the null hypothesis that the sample does not have different weights on average than the population of metal discs? Suppose that a sample of size 50 has the mean weight of 118 g. Ī company produces metal discs with a mean weight of 120 g and standard deviation of 30 g. If the Z-test statistic is greater than this critical value, then this may provide evidence for rejecting the null hypothesis. For example, the significance level α = 0.01, has a critical value of 2.326. Where, s is the population standard deviation and n is the sample size.įor each significance level, α, the Z-test has a critical value. Where, x is the sample mean, m is the population mean, and SE is the standard error, which can be calculated using the following formula: To calculate a Z-test statistic, the following formula can be used:
In cases where the population variance is unknown, or the sample size is less than 30, the Student's t-test may be more appropriate. The population is assumed to be normally distributed The variance of the sample is assumed to be the same as the population
The mean of the sample distribution is known The mean and standard deviation of the population distribution are known Two sample Z-tests are more appropriate for comparing the means of two samples of data. One sample Z-tests are useful when a sample is being compared to a population, such as testing the hypothesis that the distribution of the test statistic follows a normal distribution. The Z-test is used to compare means of two distributions with known variance.


 0 kommentar(er)
0 kommentar(er)
